Slope Y-Intercept Form to Standard Form

My students are having some trouble with changing slope y-intercept form of a line to standard form and vice versa. You must first understand solving equations before this will make sense. Having a good grasp of variables on both sides of the equation will help since it involves moving a variable term from one side of the equation to the other.

Here is an example:

Rewrite y = 2x - 5 (slope y-intercept form) as standard form.

Move the 2x to the left side of the equation with the y. -2x + y = -5

That is all that is required for this one. It is now in standard form (Ax + By = C).

Another part of the assignment that we worked on required that the standard form be written with integers (no fractions).

Rewrite 3/5y = 2/3x + 2 in standard form using integers.

Move the x term to the left side of the equation. -2/3x + 3/5y = 2
Now to get rid of the fractions, you will multiply both sides of the equation! by 15 (the least common multiple of 3 and 5). You could multiply by any multiple of 3 and 5 but generally we use the least common multiple. As long as this multiplication is done to BOTH sides, the equation will stay balanced. Hint: Remember that you must use the distributive property on the left side of the equation.

15[-2/3x + 3/5y] = 2(15)

-30/3x + 45/5y = 30

-10x + 9y = 30 (standard form using integers)

find the y intercept

Remainder Theorem and The Rational Roots Theorem

Today in class, we went over one more time how to do synthetic division and how to find the roots of a function using the Remainder Theorem.

After that, we learned how to find the missing coefficient in a polynomial if we already know what the remainder is. Here's how you would do this:

Let's say you have the question:


The first thing you want to do is write it out in a way that is easy to understand:


Then you plug the root of the denominator into the function:


Since we already know the remainder we can rewrite it this way:


Now all we do is isolate K with a little algebra, and solve it:


And there you have it!

Near the end of the class we managed to quickly learn the Rational Roots Theorem. This theorem allow! s us to find any rational roots of a polynomial function. Here's an example:

So you're given the equation:


The first thing to do is the find all the possible positive and negative factors of the constant term:


Now we find all the positive factors of the leading coefficient:


We then list all the possible rational roots, eliminating any duplicates:


We can then test out these roots by using synthetic division and the factor theorem to turn the function into a quadratic (Remember: If the remainder is 0, then it is a root):


This then gives you:


Now you just factor the equation and find the roots:


And there you have it! That's about all we did for today, tomorrow's scribe will be...Niwatori-san

factor theorem calculator

Canvas size and proportion

Franz Xavier Winterhalter 1805-1873 Madame Rimsky Korsikov

I am illustrating tonight's posts with the art of Franz Winterhalter, who was a fashionable portrait painter to the royalty of 19th century Europe. He has been derided as superficial and overly flattering to his sitters, but I have always enjoyed his technical virtuosity. He paints flawless textures and I like his color. I can't claim he has anything to do within tonight's subject but I like to show art in nearly eve! ry post.The images were, of course, provided by our friends over at art renewal .org.

I am going to write tonight about selecting canvas sizes on which to paint .
I suggest that you paint only about six different sizes and stick to stock sizes when you paint. The advantage of stock or common sizes is that you don't necessarily have to have all of your frames custom made, but can instead buy them off the rack. Here are some of the most common stock sizes for frames. Artists specify frames using the height first by the width, they would say for example, 24 by 36. A 36 by 24 is a vertical. My friend from Maine, painter Scott Moore insists "if God had meant for us to paint verticals he would have placed one of our eyes above the other".
Here are the smaller sizes;

• 5 x 7
• 8 x1 0
• 9 x 12
• 1 1x 14
• 12 x 16

The most common middle sizes are;

• 16 x 20
• 18 x2 4
• 20 x2 4

The large! r sizes are;

• 24 x 30
• 24 x 36
• 30 x! 40

If you choose two sizes from each of these categories, one elongated and one more square, you will have six sizes. You should be able to find premade frames for those sizes from almost any supplier. If you want to have custom frames made, by which I mean closed corner 22k. gold frames, you will be happy to be able to put the picture into a ready made frame. That's a good thing for when you send it to a show or gallery where you know your paintings will be stacked by tongue swallowing interns. Here are some sizes that although less common are in routine use in the trade:

• 14 x 18
• 22 x 28, Sargents usual non-portrait size
• 20 x 30
• 30 x 36
• Sometimes artists use what are called double squares such as 12 x 24, or 24 x 48, etc. There isnt really a standard size double square, but they are nice for panoramic pictures.
  

There's another Winterhalter, isn't that lovely? Shes a countess, looks real high maintenance to me.

Artists I know often paint these sizes but you can't generally expect to find a premade frame for these sizes. You will save a lot of headaches by limiting yourself to six sizes. Having interchangeable framing is real handy. I have actually considered this summer only painting three sizes. 16 x 20, 18 x 24, 24 x 30.

Often times t! he proportion you choose for a painting is a function of how d! eep the view you are painting is. In the woods I am liable to choose a more square shape. Along the shore where there is a great expanse of distance I am likely to choose a wider shape.
When you hear hucksters on the radio advertising "over the sofa" sized oils, they mean a 24x36. That's a great landscape size just the same..

There's a story I heard concerning painting sizes. A well known artist visited one of his galleries unannounced and his painting wasn't hanging. But his frame was. The unscrupulous dealer had taken the frame he had bought for his own painting and put it on a painting by another artist. After that he often sent galleries odd sizes, instead of a 24 x 36 he would send them a 24 x 34, and that solved that problem!

I should tell you, that I don't quite obey this six size rule myself, I paint 26x29 canvasses. I have done lots of them. That's a size I got from Willard Metcalf. I find it designs really well for me and it has a delicacy of siz! e and shape that I like. I usually have to special order those 29 inch stretchers. I have never seen a 26x29 from anybody else except for Metcalf. Wetcalf was raised in a spiritualist family. That was a common religion in the late 19th century. Often they would hold seances and try to communicate with the dead. They were interested in mystical numerology too. I think this size may have come from Willards interest in numerology, but I don't really know that. But 29 is a prime number and 26 is twice 13, another prime number. I just like the way I can design the shape, maybe it is magic.

Empress Marie Alexandrova of Russia. Love the dress. I wish women dressed that way today. I don't guess its ever coming back though. What fun it must have been for portrait painters then.

I make between 40 and 70 paintings a year, I throw about a third as many more away unfinished because they have some sort of an irredeemable flaw. So if I paint too many sizes it really gets complicated and expensive having many dedicated frames that only fit one painting.
Tomorrow I will talk more about things to paint on.

direct square proportion

Coat of Arms.

Make Your Coat of Arms allows you to easily create your own family coat of arms or family crest based on your family ancestry or on the values that are important to you and your family today.


[ Coat of Arms ]

Here's another [ Coat of Arms ] generator. (via Pitoche)

coat of arms generator

Impact Factors - The Basics

Impact Factors - The Basics - Part 1 (Cross 2008) is an explanatory guide to Impact Factors [IFs] from by Taylor & Francis. It does in fact cover the basics, what impact factors are and how they are calculated. However, it goes into greater detail on the very important topic of Subject Variation within Impact Factors including some very helpful graphs to illustrate the point. Here are some of the key figures made:

• Average category impact factors for Economics, Nursing, Education & Educational Research and Business are all less then one. This compares with the top category of Cell Biology at c5.7


• The coverage of journals in the Social Sciences by the Journals Citation Reports [JCR] are significantly less that the Sciences. For example Economics c 42% and Business and Management c33%. This compares with the top category Physics a! t c83%


• The rates of citing in the Impact Factor Window (2 years) are higher in the Sciences, for example Cell Biology 22% compared with Economics at 8%

These figures provide a big health warning to comparing IFs even between apparently related subjects - there is also variation within subjects. The guide is just 7 pages long and worth a read especially for those researching in arts, humanities and social sciences who may wonder at the comparatively higher IFs of scientific colleagues.


References

Cross, J., 2008. Impact Factors - The Basics - Part 1. London: Taylor & Francis. Available from: http://www.tandf.co.uk/libsite/newsletter/issue9/Back_to_Basics.pdf [Accessed: 17 June 2008].

Links

Journal Citation Reports [JCR] which publishes IF's is available here. It i! s ATHENS Authenticated.

basics of factors

The problem with word problems 2

For the purpose of this post, we could divide word problems to three different categories:
1) routine word problems
2) non-routine word problems
3) algebra word problems

Actually you could divide algebra word problems to routine and non-routine as well, but I want to now talk about word problems kids encounter in school before algebra - in grades 1-8 usually.

J.D. Fisher suggested in the comments section of my previous post on word problems that kids are encouraged to think linearly, step-by-step. Then, when the word problems they encounter don't anymore follow any step-by-step recipe, they are lost. You might want to go back and read that.

Don't typical math book lessons kind of follow this recipe:

LESSON X
---------------------
Explanation and examples.
Numerical exercises.
A few word problem! s.

In other words, the word problems are usually in the end of the lesson. (That might make solving them a rush.)

Then, have you ever noticed... If the lesson is about topic X, then the word problems are about the topic X too!

For example, if the topic in the lesson is long division, then the word problems found in the lesson are extremely likely to be solved by long division.

And, typically the word problems only have two numbers in them. So, even if you didn't understand a word in the word problem, you might be able to do it. Just try: let's say that the following made-up problem is found within a long division lesson. Can you solve it?

La tienda tiene 870 sabanas en 9 colores diferentes. Hay la misma cantidad en cada color. Cuantos sabanas de cada color tiene la tienda?

My thought is that over the years, when kids are exposed to such lessons over and over again, they kind of figur! e it out that it's mentally less demanding just not even read ! the prob lem too carefully. Why bother? Just take the two numbers and divide (or multiply, or add, or subtract) them and that's it.

I'm not saying that such word problems are not needed in the end of division lessons. I'm sure they have their place. But too much of those simple 'routine' problems can be a problem... I feel kids then "learn" a rule: "Word problems found in math books are solved by some routine or rule that you find in the beginning of the corresponding lesson."

It might teach their minds to be lazy and not willing to tackle non-routine problems.

Maybe it would help to give students a bunch of short routine word problems, and NOT ask them to find answer. Instead, ask them to tell what operation(s) are needed to find the answer.

Maybe it would help to have separate lessons with mixed word problems, including some non-routine, an! d devote some time to them.

I'm curious to hear your thoughts on this.

And, lastly some (most are free) word problem resources if you need more than what's in your math book:

Word problems for kids
A great selection of word problems for grades 5-12. A hint and a complete solution available for each problem.

Aunty Math
Math challenges in a form of short stories for K-5 learners posted bi-weekly.

Problem of the Week home page
Links to 'problem of the week' websites organized by grade levels. These are excellent for finding more challenging problems and to motivate.

Primary Mathe! matics Challenging Word Problems
For grades 1-6 from ! Singapor e Math. The books include answer key, worked examples, practice problems, and challenging problems. About $8 per book.

I have some more resources listed at my own site.

Tags: math, elementary, curriculum

algebra word problem solver

Triangle Congruence Theorems

are so boring, and there is no nice way to teach them. A google search turns up a hojillion versions of "state the theorem and show an example." Here's what I did this year. It sucks and I'm looking for better ideas.

What makes triangles congruent? They're the same size and shape. This means all the sides and all the angles are congruent. The kids had to sit through one proof like this. What a pain, having to write 6 statements to show that two triangles are congruent.

In class the next day, I had them draw three segments with a ruler on scrap paper: one the length of their index finger, one the length of their ear, and one the width of their palm. I told them to construct a triangle with sides of these three lengths. I passed out compasses but didn't give them any instruction on how to do it. Some of them figured it out. A few of these guys showed everyone what they did with the giant compass and yardstick on the whiteboard.

We had a "discussion" about how there was only one triangle you could make with the three lengths. And when I say "discussion" I mean I said - did you notice that those three lengths would only make one triangle? That the angles were sort of 'locked in'? You couldn't just draw the other sides at any old angle? Then I did a lame little demo of how with 4 sticks, the angles are all wobbly and you can make a ton of different quadrilaterals, but with three sticks, you can only get them to make one triangle. I said something about bridges. Then I modeled and they practiced a bunch of SSS proofs.

Today was SAS. In previous years I passed out protractors, and asked them to draw a triangle with two specific side lengths and a specific included angle, then look around and notice how everyone ended up with the same triangle. I didn't feel this really sent the message that the angle has to be included. This year, I asked them to solve these two problems:

I don't honestly know how effective this was. Yeah "we" eventually made the point, but it took FOREVER, and I'm sure some kids got the point, but I'm also sure that half the class was just sitting politely waiting for the torture to be over. And some kids, of course, get downright indignant when you ask them to do something that turns out to be impossible. Which, whatever, but it's much harder to teach somebody who has concluded you are a crap teacher.

Then we practiced determining which other pair of corresponding things you would need in order to use SAS, then we did one example proof.

I know this sucks but I don't know anyone doing anything better. So let me hear it, hot shots.

Theorem on Area of Triangle

find the slope for the graph of the equation

Before we know how to find the slope for the graph of the equation ,lets see what is slope.

Slope is used to describe the steepness, incline, gradient, or grade of a straight line. A higher slope value indicates a steeper incline. The slope is defined as the ratio of the "rise" divided by the "run" between two points on a line, or in other words, the ratio of the altitude change to the horizontal distance between any two points on the line. It is also always the same thing as how many rises in one run.

Using calculus, one can calculate the slope of the tangent to a curve at a point.

The concept of slope, and much of this article, applies directly to grades or gradients in geography and civil engineering.

Question:-

Draw the graph of 2x-3y=12. Use the graph to find the slope of line and area between the axes.

Answer:-

This Online help with math shows us ,how to draw the graph for the above problem.

by simplifying the equation we get.

y=0, x=6
y=-2, x=3
y=-4, x=0

We also use the slope formula to get the slope on the line .

Equation of the tangent to the curve

Vectors and Matrices - 3

Now, I'll write about specific functions for matrices.

The most common functions that I use:

• eye(m,n) - identity matrix;
• zeros(m,n) - matrix of zeros;
• ones(m,n) - matrix of ones;
  
• det(X) - determinant;
  
• inv(X) - matrix inverse;
• pinv(A,[tol]) - pseudoinverse;
• sum(x,[key]) - sum (row sum, column sum) of vector/matrix entries;
• prod(x,[key]) - product (row sum, column sum) of vector/matrix entries;
• mean(x,[key]) - mean (row sum, column sum) of vector/matrix entries;
• stdev(x,[key]) - standard deviation (row sum, column sum) of vector/matrix entries;
• geomean(x,[key]) - geometric mean (row sum, column sum) of vector/matrix entries;
• harmean(x,[key]) - harmonic mean (row sum, column sum) of vector/matrix entries;
• msd(x,[key]) - mean squared deviation (row sum, column sum) of vector/matrix entries;
• rand(m1,m2,.. [,key]) - random number generat! or;
• grand(m, n, dist_type [,p1,...,pk]) - Random number generator(s);
• find(X) - find indices of boolean vector or matrix true elements.
  

Each function has it own purpose.

Let's play, with them.

-->eye(3,3) // identity matrix 3 lines and 3 columns*
ans =

1. 0. 0.
0. 1. 0.
0. 0. 1.

-->rand(5,2) // matrix (5 lines and 2 columns) of random numbers with uniform probability distribution between [0,1]
ans =

0.0683740 0.5442573
0.5608486 0.2320748
0.6623569 0.2312237
0.7263507 0.2164633
0.1985144 0.8833888

-->rand(2,5,'normal') // matrix (2 lines and 5 columns) of random numbers with normal (Gaussian) distribution (mean = 0 and variance = 1)
ans =

1.0478272 - 1.4061926 - 1.7350313 - 0.2143931 2.5891773
- 1.3218008 - 1.0384734 0.5546874 - 2.0735088 0.0424792

-->det(eye(4,4)) // determinant of identity matrix 4 x! 4
ans =

1.

-->X = rand(5,5) // X is a matrix (5 x 5) with random values between [0,1]
X =

0.4368588 0.0437334 0.1280058 0.1531217 0.8784126
0.2693125 0.4818509 0.7783129 0.6970851 0.1138360
0.6325745 0.2639556 0.2119030 0.8415518 0.1998338
0.4051954 0.4148104 0.1121355 0.4062025 0.5618661
0.9184708 0.2806498 0.6856896 0.4094825 0.5896177

-->det_X = det(X) // det_X is the determinant of X
det_X =

- 0.0799884

-->[py px] = find(eye(3,3)) // px is the positions (x-coordinates) of numbers nonzeros and py is the positions (y-coordinates) of numbers nonzeros
px =

1. 2. 3.
py =

1. 2. 3.

-->[py px] = find(~eye(3,3)) // the ~ is the logic negative operation, so (~0) = 1 and (~1) = 0**
px =

1. 1. 2. 2. 3. 3.
py =
2. 3. 1. 3. 1. 2.


-->X // the variable X (X = rand(5,5))
X =

0.4368588 0.0437334 0.1280058 0.1531217 0.8784126
0.2693125 0.4818509 0.7783129 0.6970851 0.1138360
0.6325745 0.2639556 0.2119030 0.8415518 0.1998338
0.4051954 0.4148104 0.1121355 0.4062025 0.5618661
0.9184708 0.2806498 0.6856896 0.4094825 0.5896177

-->sum(X,'r') // sum over the columns of X (row of values)
ans =

2.6624119 1.4850001 1.9160468 2.5074436 2.3435661

-->sum(X,'c') // sum over the lines of X (column of values)
ans =

1.6401323
2.3403973
2.1498187
1.9002098
2.8839105

-->sum(X) // sum of all elements of X
ans =

10.914469


So, if anyone has any question, then everyone can do comments.

----------

* If! you do a command without send the return to a variable, then ! the Scil ab creates the variable ans (answer) with the return or function or operation.

For example:

-->1+1
ans =

2.

-->cos(%pi)
ans =

- 1.

-->sin(%pi/2)+1
ans =

2.



** I'll write about logic operations in next posts.

3 sum positions

Subsets and Value Sets

The HITFACA Blog reports:
On February 23, 2010, the Vocabulary Task Force established by the Clinical Operations Workgroup of the Health IT Standards Committee will hold a public hearing on “Vocabulary Subsets and Value Sets” as facilitators of meaningful use of electronic health records (EHRs).

And then provides a list of questions which I've responded to below:

1. Who should determine Subsets and/or value sets that are needed?
   It depends.  Subsets or value sets are needed for implementation guides and for much broader use cases such as Laboratory ordering and Results.  Consensus standards organizations should be responsible for determining which Subsets or value sets are needed for their implementation guides.  Broader use cases may be driven by various initiatives at regional or national levels.  An organization responsible for harmonization of standards similar to ANSI/HITSP should also have a role in identifying value sets.
2. Who should produce Subsets and/or value sets?
   Consensus based Standards bodies should produce and MAINTAIN them.  Production seems easy, but a value set or subset that has no maintenance process has no life.  
3. Who should review and approve Subsets and/or value sets?
   It depends upon what they are used for.  Primarily the concensus groups of the producer organizations, but in some cases, such as value sets used for quality measures, review and approval could also include organizations like NCQA. 
4. How should Subsets and/or value sets be described, i.e., what is the minimum set of metadata needed?
   See HITSP TN903: Data Architecture Technical Note
5. In what format(s) and via what mechanisms should Subsets and/or value sets be distributed?
   Value sets should be available in a standard format, such as the Rich Release format used by NLM for RxNORM and UMLS.
6. How and how frequently should Subsets and/or value sets be updated, and how should updates be coordinated?
   It depends on their use.  Updates for fairly static value sets should be reviewed at least every five years (ANSI rules uses this figure for reaffirmation of Standards).  Value sets for clinical use should be reviewed and updated at least annually.  Some value sets and Subsets may need to be updated quarterly, montly or even weekly (e.g., medications).  Updates may be delivered as a subset containing only the changes in more frequently updated value sets.
7. What support services would promote and facilitate their use?
   Value sets should be available from a Web Service, such as that described in the HITSP T66 Retrieve Value Set Transaction.
8. What best practices/lessons learned have you learned, or what problems have you learned to avoid, regarding vocabulary subset and value set creation, maintenance, dissemination, and support services?
   Building a value set requires a commitment to ongoing maintenance of it.  Dissemination should support both manual download automated retrieval and update.  Support services require that there be a feedback mechanism (such as an e-mail list service) to comment on it.  Public input is absolutely necessary in the creation and maintenance of a value set.  Quick response may be needed for clinical value sets to address issues like H1N1 or new medications or treatment options.
9. Do you have other advice or comments on convenience Subsets and/or value sets and their relationship to meaningful use?
   Isn't this enough...
10. What must the federal government do or not do with regard to the above, and/or what role should the federal government play?
    The Federal Government should have a role in the coordination of value set deployment activities.  Presently the CDC, NLM and AHRQ (USHIK) all have some role in the development or deployment of value sets, which includes overlapping distribution, delivery and maintenance responsibilities.  Duplication of these efforts is not useful.  It would be better if there was a single coordinated effort, which could include participation from all of these bodies.
    NLM has appropriate infrastructures for manual download, licensing and deployment.  CDC has appropriate infrastructures for some development of public health oriented value sets.  USHIK has appropriate infrastructures for delivery of knowledge about value sets (e.g., metadata).  To my knowledge, none of these provide for automated computer update of value sets using simple web services such as those described in the HITSP T66 Retrieve Value Set Transaction, but I believe CDC is closest to having that capability.

Subsets

How to find slope intercept

Introduction:

     An area of surface that tends evenly towards top or down is called as slope. The slope of a line in the plane containing the x and y axes is generally represented by the letter m, and is defined as the change in the y coordinate divided by the corresponding change in the x coordinate, between two distinct points on the line. For finding slope intercept we need to know the following things.

Finding Slope Intercept Form:

Slope intercepts form:

The standard form of a line is,

ax+by+c=0    

We can express the line as slope intercept form. The Slope Intercept Form of a line is,

y=mx+b, Where m is slope of a line and b is y-intercept of a line.

Finding slope Intercept:

When two points are given, we can use the following formula to find the Slope Intercept Form of a line,

(y-y1)=m(x-x1), where m is slope,(x1,y1) is one point in the line

The slope m can be obtained by using ! the fol lowing formula,

m= (y2-y1)/(x2-x1), here (x1, y1) and (x2, y2) are the

points in a line or segment.

Or

y-y1/y2-y1=x-x1/x2-x1

Hope you like the above explanation. Please leave your comments, if you have any doubts.

Slope Intercept Form

Baluster End Spacing Calculator in C#

I'm working on putting up balusters (spindles) on my deck at home, and since all the posts are spaced differently, I needed to calculate the proper end spacing for each section. Granted, it's easy enough to do this by guessing at the first length, then physically marking out each baluster width and spacing on the actual deck, and then adding the start spacing with the end spacing and dividing by two. And that's probably what I'd normally do, but I wanted to take a little break, so I made a quick app to figure this out for me.

It's a very simple app, and took about 10 minutes to write, but here's the interesting parts in case anyone is interested:

/// <summary>
/// Determines the number of balusters needed based on the top railing width
/// </summary>
/// <returns>Baluster count</returns>
public int CalculateBalustersNeeded() {
    int numberOfBalusters = Convert.ToInt32(Math.Ceiling(
(this.topRailingWidth - this.spacing) / (this.balusterWidth + this.spacing)));

    return numberOfBalusters;
}

and

/// <summary>
/// Determines the spacing between the post and the baluster.
/// </summary>
/// <param name="balusterCount"># of balusters used.</param>
/// <returns>Spacing at each end in inches</returns!  >
public f loat CalculateEndSpacing(int balusterCount) {
    //all balusters + spacing without end spacing
    float totalUnitWidth = (balusterCount * this.balusterWidth)
+ (this.spacing * (balusterCount - 1));
    float endSpacing = (this.topRailingWidth - totalUnitWidth) / 2;

    return endSpacing;
}

Nothing too exciting, really. And Excel probably would have been a better choice than a console app. But since it's all done with more or less "proper" objects (these methods are part of a "RailingSection" class generic collection that's part of a "Deck" object), I can now easily expand this into a full-blown deck design software package. Right. I guess I just can't get enough of coding at work...

UPDATE (6/13): Wow, this post ! is getting a lot of hits by people searching for a baluster calculator - here's the compiled EXE file: BalusterCalc.exe. You'll need the .NET framework 2.0 or higher to run it.

5 number summary online calculator

Negative Binomial Coefficient

While reading through a book on probability and calculating the expectation of geometric series, I came across an interesting sum
We know that if then the sum converges to


Coming from the other side and using binomial theorem we getwhich expands to



Which leads to an interesting conclusion

I got maxima to verify this by calling the binomial function for various combinations of -1 and n. I am a little confused about the interpretation of the meaning though

Usually nC2 is used to imply from "n" objects, choose 2 at a time. nC2 gives us the number of total such combinations. What does -1Cn mean? What are the other proofs for -1Cn?

binomial coefficient

Accelerated Change of HW

Thursday, 12/10

Only do the HW on pg 99 #22-27 all. Skip #28-36.

Quiz on Friday

Bring your Final Review worksheet with you on Friday to work on after the Quiz. See you tomorrow!

Multiplying and Dividing radicals

Do you need drill to learn multiplication facts?

Continuing on the same lines as my previous post, what about multiplication facts and drill?

Well, the principle is similar: show them first the concept and patterns.

Then can come some plain drill.

But, I want to share with you a few more detailed points.

1. The main "patterns" in various multiplication tables of course follow from the concept of multiplication. For example, table of 2 is counting by 2's. You get table of 4 by doubling the answers in table of 2. You get table of 8 by doubling the answers in table of 4.
   
   Table of 10 is counting by 10s. Table of 5 - just take half of what the 10 ×
   
   Here are some resources to give you ideas about these kind of patterns and little "tricks".
   
   * Michele's Math
   * Times! Tables' factsheets
   
   


2. We ALSO need them to know the tables "backwards".
   
   Let me explain.
   
   It's not enough to know that 8 × 7 is 56, when someone asks what is 8 × 7. The students ALSO need to know that 56 is 8 × 7, when given just the answer 56.
   
   This is very important. Students need this fairly soon when they start learning division. Later on it will be important when simplifying fractions or factoring.
   



3. Since it's important to know the tables backwards, I do not feel it's enough if the child is able to "figure out" the multiplication problems. I feel they need to memorize them, period, and not just be able to count or use some other method to find the answers.
   
   It's fine initially, and indeed very helpful, if the child figures out 8 × 8 by first going 8 × 2 and doubling that twice.
   
   But this fact also needs memorized so that later on, wh! en she comes to the problem 64 ÷ 8, it won't take her 10 ! seconds to find the answer.
   
   Now you might ask why is that important? Because of long division, for example. It's going to be a pain to learn long division if you don't know your division facts by heart.
   
   Here's another reason: soon the student is going to have fractions to simplify. If you know your division facts, then simplifying 35/56 will be a breeze, otherwise a pain.
   

See how it all builds on the previous topics? You need to get a good foundation, and multiplication facts "both ways" is part of that foundation.

I have posted online the entire guide to effective oral drilling from one of my books.

The guide explains how the teacher and student can achieve memorizing multiplication tables in this manner where they know the answers and they know which answer goes with which multiplication problem.

Check also a list of online games that practice times tables. These are great after you've done some basic drill and the child needs reinforcement (practice!!!).

Multiplication math tables examples

Least Common Multiple (LCM)

The least common multiple (LCM) is the smallest positive integer that is a multiple both of a and of b. You can also find the LCM of more than two integers. This is a key topic to understand in order to add and subtract fractions with ease.

The easiest way to find the LCM of two or more integers is to start by multiplying the number by 1, then by 2, then by 3, etc. In the process, you are making a list of the multiples of each number. The LCM is the lowest number that appears in ALL lists. Let’s do an example by finding the LCM of 8 and 10.

multiples of 8 = 8, 16, 24, 32, 40, …
multiples of 10 = 10, 20, 30, 40, 50, …

One can easily see that 40 is the lowest number that appears in BOTH lists. To do much tougher LCM problems, check out this LCM calculator which will also calculate the GCF (greatest common factor) at The least common multiple (LCM) is the smallest positive integer that is a multiple both of a and o! f b. You can also find the LCM of more than two integers. This is a key topic to understand in order to add and subtract fractions with ease.

The easiest way to find the LCM of two or more integers is to start by multiplying the number by 1, then by 2, then by 3, etc. In the process, you are making a list of the multiples of each number. The LCM is the lowest number that appears in ALL lists. Let’s do an example by finding the LCM of 8 and 10.

multiples of 8 = 8, 16, 24, 32, 40, …
multiples of 10 = 10, 20, 30, 40, 50, …

One can easily see that 40 is the lowest number that appears in BOTH lists. To do much tougher LCM problems, check out this LCM calculator which will also calculate GCF (greatest common factor) at http://www.mathematicsmagazine.com/applications/GCF_LCM.htm .

least common multiple lcm

Three Dimensional Poisson's Equation

This is a follow up to the post I wrote a while back about implementing numerical methods. The goal is to demonstrate a work-flow using tools that come included in the Fedora Linux (and many other) distributions.

1. In Maxima
   
   • Define governing equations
     
   • Substitute finite difference expressions for differential expressions in the governing equations
     
   • Output appropriate difference expressions to Fortran using f90()
     
2. In Fortran: wrap the expression generated by Maxima in appropriate functions, subroutines and modules
   
   
3. In Python
   
   • Compile modules with f2py, which comes packaged along with numpy
     
   • Write the high-level application code, parsing input decks, performing optimization, grid convergence studies, or visualizations that use the compiled Fortran modules
     

Maxima

The governing equation is the three-dimensional Poisson's equation. In Cartesian coordinates The Maxima code to defi! ne this equation is straightforward:

depends(u,x); depends(u,y); depends(u,z); /* Poisson's equation: */ p : 'diff(u,x,2) + 'diff(u,y,2) + 'diff(u,z,2) = -f;

Now that we have the continuous differential equation defined we can decide on what sort of discrete approximation we are going to solve. The simple thing to do with second derivatives is to use central differences of second order accuracy, which require only information from closest neighbours in the finite difference grid. Replacing the differential expressions with difference expressions is accomplished in Maxima with the ratsubst() function.

/* substitue difference expressions for differential ones: */
p : ratsubst((u[i-1,j,k] - 2*u[i,j,k] + u[i+1,j,k])/dx**2 , 'diff(u,x,2), p);
p : ratsubst((u[i,j-1,k] - 2*u[i,j,k] + u[i,j+1,k])/dy**2 , 'diff(u,y,2), p);
p : ratsubst((u[i,j,k-1] - 2*u[i,j,k] + u[i,j,k+1])/dz**2 , 'diff(u,z,2), p);
/* substitute the correct array value of f:*/
p : ratsubst(f[i,j,k], f, p);

This assumes that the solution u and the forcing function f are stored in three dimensional arrays, if not then the indexing in the difference expressions becomes more complicated. If we want to apply a Gauss-Seidel method to solve our elliptic problem we just need to solve p for u[i,j,k], and then dump that expression to Fortran format.

gs : solve(p, u[i,j,k]);
del : part(gs[1],2) - u[i,j,k];
/* output for fortran: */
with_stdout("gs.f90", f90(d = expand(del)));

This gives the expression for the update to the solution at each iteration of the solver.

Fortran

The Maxima expressions developed above need control flow added so they get applied properly to our solution array.

do k = 1, nz
do j = 1, ny
do i = 1, nx
d = (dy**2*dz**2*u(i+1,j,k)+dx**2*dz**2*u(i,j+1,k)+dx**2*dy**2* & u(i,j,k+1)+dx**2*dy**2*dz**2*f(i,j,k)+dx**2*dy**2* & u(i,j,k-1)+dx**2*dz**2*u(i,j-1,k)+dy**2*dz**2*u(i-1,j,k))/ & ((2*dy**2+2*dx**2)*dz**2+2*dx**2*dy**2)-u(i,j,k) u(i,j,k) = u(i,j,k) + w*d
end do
end do
end do

The expression for the update was generated from our governing equations in Maxima, one of the things to notice is the w that multiplies our update, this is so we can do successive over relaxation. Also, we'll go ahead and package several of these iterative schemes into a Fortran module

module iter_schemes
implicit none
contains

...bunches of related subroutines and functions ...

end module iter_schemes

Python

Now we want to be able to call our Fortran solution schemes from Python. Using F2py makes this quite simple:

[command-line]$ f2py -m iter_schemes -c iter_schemes.f90

This should result in a python module iter_schemes.so that can be imported just as any other module.

import numpy
from iter_schemes import *

... do some cool stuff with our new module in Python ...

Conclusion

This approach might seem like over-kill for the fairly simple scalar equation we used, but think about the complicated update expressions that can be generated for large vector partial differential equations like the Navier-Stokes or Maxwell's equations. Having these expressions automatically generated and ready to be wrapped in loops can save lots of initial development and subsequent debugging time. It also makes generating unit tests easier, and so encourages good development practice. But does it work? Of course, here's the convergence of the Gauss-Seidel and SOR schemes discussed above along with a Ja! cobi scheme and a conjugate gradient scheme applied to a 50 by 50 by 50 grid with a manufactured solution. The plot was generated with the Python module matplotlib.

solve a homogeneous differential equation

Calculator with GUI

I started playing around with the Factor GUI framework recently. The documentation is very detailed, but sometimes it is nice to have simple examples to learn from.

I thought it would be fun to build a simple calculator application. A teaser of what it will look like when we are done:

First, some imports and a namespace.

USING: accessors colors.constants combinators.smart kernel fry math math.parser models namespaces sequences ui ui.gadgets ui.gadgets.borders ui.gadgets.buttons ui.gadgets.labels ui.gadgets.tracks ui.pens.solid ;  FROM: models => change-model ;  IN: calc-ui

Note: we have to specifically import change-model from the models vocabulary, since it might conflict with an accessor.

Factor user interface elements are called gadgets. Many of them support being dynamically updated by being connected to models. Each model maintains a list of connections that should be updated when the value being held by the model changes.

The Model

Our calculator model is based on the notion that we have two numbers (x and y) and an operator that can be applied to produce a new value.

TUPLE: calculator < model x y op valid ;  : <calculator> ( -- model )     "0" calculator new-model 0 >>x ;

If we want to reset the model (such as when we press the "clear" button):

: reset ( model -- )     0 >>x f >>y f >>op f >>valid "0" swap set-model ;

We're storing all values as floating-point numbers, but (for display purposes) we'll show integers when possible:

: display ( n -- str )     >float number>string dup ".0" tail? [         dup length 2 - head     ] when ;

Each of x and y can be set based on the value, and the op is specified as a quotation:

: set-x ( model -- model )     dup value>> string>number >>x ;  : set-y ( model -- model )     dup value>> string>number >>y ;  : set-op ( model quot: ( x y -- z ) -- )     >>op set-x f >>y f >>valid drop ;

Pushing the "=" button triggers the calculation:

: (solve) ( model -- )     dup [ x>> ] [ y>> ] [ op>> ] tri call( x y -- z )     [ >>x ] keep display swap set-model ;  : solve ( model -- )     dup op>> [ dup y>> [ set-y ] unless (solve) ] [ drop ] if ;

We support negating the number:

: negate ( model -- )     dup valid>> [         dup value>> "-" head?         [ [ 1 tail ] change-model ]         [ [ "-" prepend ] change-model ] if     ] [ drop ] if ;

And pushing the "." button (to add a decimal), or a number (to add a digit):

: decimal ( model -- )     dup valid>>     [ [ dup "." subseq? [ "." append ] unless ] change-model ]     [ t >>valid "0." swap set-model ] if ;  : digit ( n model -- )     dup valid>>     [ swap [ append ] curry change-model ]     [ t >>valid set-model ] if ;

That pretty much rounds out the basic features of the model.

The GUI

For convenience, I store the calculator model in a global symbol:

SYMBOL: calc <calculator> calc set-global

I can use that to create buttons for each type (using short names and unicode characters to make the code a bit prettier):

: [C] ( -- button )     "C" calc get-global '[ drop _ reset ] <border-button> ;  : [±] ( -- button )     "±" calc get-global '[ drop _ negate ] <border-button> ;  : [+] ( -- button )     "+" calc get-global '[ drop _ [ + ] set-op ] <border-button> ;  : [-] ( -- button )     "-" calc get-global '[ drop _ [ - ] set-op ] <border-button> ;  : [×] ( -- button )     "×" calc get-global '[ drop _ [ * ] set-op ] <border-button> ;  : [÷] ( -- button )     "÷" calc get-global '[ drop _ [ / ] set-op ] <border-button> ;  : [=] ( -- button )     "=" calc get-global '[ drop _ solve ] <border-button> ;  : [.] ( -- button )     "." calc get-global '[ drop _ decimal ] <border-button> ;  : [#] ( n -- button )     dup calc get-global '[ drop _ _ digit ] <border-button> ;  : [_] ( -- label )     "" <label> ;

We will create a label that is updated when the model changes.

: <display> ( -- label )     calc get-global <label-control> { 5 5 } <border>         { 1 1/2 } >>align         COLOR: gray <solid> >>boundary ;

And, finally, creating the GUI (using vertical and horizontal track layouts):

: <col> ( quot -- track )     vertical <track> 1 >>fill { 5 5 } >>gap     swap output>array [ 1 track-add ] each ; inline  : <row> ( quot -- track )     horizontal <track> 1 >>fill { 5 5 } >>gap     swap output>array [ 1 track-add ] each ; inline  : calc-ui ( -- )     [         <display>         [     [C]     [±]     [÷]    [×] ] <row>         [ "7" [#] "8" [#] "9" [#]    [-] ] <row>         [ "4" [#] "5" [#] "6" [#]    [+] ] <row>         [ "1" [#] "2" [#] "3" [#]    [=] ] <row>         [ "0" [#]     [.]     [_]    [_] ] <row>     ] <col> { 10 10 } <border> "Calculator" open-window ;  MAIN: calc-ui

Then, running the calculator application:

( scratchpad ) "calc-ui" run

The code for this is on my Github.

factorization calculator

Help on Polynomial Factoring Calculator

Introduction to learn factor polynomials calculator:

In this article let me help you on Polynomial Factoring Calculator. It is used to solve different types of problems. It is a web-based tool designed to solve different problems.Learning factor polynomials through calculators is simple.

Factor polynomials calculator are used to understand the polynomials factorization. Given expression can be factorized by using the greatest common factor. Let us discuss about the learn factor polynomials calculator.
Steps to Learn Factor Polynomials Calculator:

The Steps to learn factor polynomials are as follows:

* Given expression can b! e arranged in the order of powers.
* Expression can be in the form of standard ax2 + bx + c = 0.
* The expression should be factorized.
* Solve the given terms.This could also help us on p value calculator

Keep reading may be in the next session let me help you on Intersection Circle

factorization calculator

Help!

Here's the deal:  I'm working on curriculum for my school and Algebra 2 is making my eyes cross.  I think the major problem is the state of Virginia is in a transition year between "old" Standards of Learning (SOLs), and "new" ones.  This year is supposed to be the year that we're still teaching and assessing the old SOLs, but we're supposed to teach the new ones, too.  Those of you that teach Algebra 2 already know that there's an enormous amount of information to cover in a short period of time.  To give you context, our school teaches it as a semester-long block course.  There's only so much a brain can handle in one day, though! 

Here's the first draft of my skills list and structure...I'm not sure what to do about the old vs. new SOLs (my skills list is based on the old SOLs because that is what will be assessed).

Note:  Gray items are not included in old or new SOLs but might be necessary for student understanding
          Blue items are being taken out of the SOLs starting next year
          Red items are new to the SOLs starting this year

Unit 1 Algebra 1 Review/Solving Equations


1 Solve multi-step equations and inequalities
2 Matrix +/-
3 Solve compound inequalities
4 Solve absolute value equations
5 Solve absolute value inequalities

Unit 2 Polynomial Review/Add Depth

6 Factor trinomial a = 1
7 Factor trinomial a > 1
8 Factor special cases (sum/diff of cubes, diff of squares, perfect square trinomials)
9 Factor out GCF first (factor completely)
10 Exponent rules
11 +/- polynomials
12 Multiply polynomials
13 Divide polynomials

Unit 3 Rational Expressions

14 Identify undefined values
15 Simplify rational expressions by factoring and canceling out common factors
16 Multiply and divide fractions
17 Multiply and divide rational expressions
18 Add and subtract fractions
19 Add and subtract rational expressions
20 Simplify complex fractions
21 Solve rational equations

Unit 4 Radicals, Radical Equations and Complex Numbers

22 Simplify numbers under radical
23 Simplify monomials under radical
24 Multiply and divide radicals
25 Add and subtract radicals
26 Nth roots to rational exponents and vice versa
27 Simplify expressions with nth roots and rational exponents
28 Solve radical equations
29 Simplify square roots with negative terms inside radical using i
30 Add and subtract complex numbers
31 Powers of i
32 Multiply complex numbers

Unit 5 Functions (intro)

33 Domain and range of relations (from ordered pairs, mapping, graph, table)
34 Identify relations that are functions and one-to-one
35 Given graph and a value k, find f(k)
36 Given graph, find zeros
37 Given graph and a value k, find where f(x)=k

Unit 6 Linear Functions


38 Slope from graph, equation, points
39 Graph from equation
40 Equation from graph
41 x- and y- intercepts
42 Determine whether lines are parallel, perpendicular, or neither from equation or graph
43 Write equations for parallel and perpendicular lines given line and point off the line
44 Graph linear inequalities

Unit 7 Systems


45 Solve systems of equations by graphing
46 Multiply Matrices using a graphing calculator
47 Inverse matrix method of systems
48 Systems of equations word problems
49 Graph systems of linear inequalities
50 Linear programming max/min problems

Unit 8 Functions (reprise)

51 Function math (addition, subtraction, multiplication, division)
52 Function composition, find a value i.e. f(g(3))
53 Function composition, find the function i.e. f(g(x))
54 Find an inverse function by switching variables

Unit 9 Quadratics

55 Graph from vertex form, identify max/min and zeros
56 Solve by factoring
57 Solve by Quadratic Formula (including complex solutions)
58 Determine roots using the discriminant
59 Write equation for quadratic given roots
60 Quadratic systems
61 Polynomials: relating x-intercept, zeroes and factors
62 End behavior for polynomials

Unit 10 Exponential/Logarithmic functions

63 Exponential growth or decay from function
64 Sketch base graph of exponential/log functions
65 Exponential to log and vice versa
66 Data analysis/curve of best fit for linear, quadratic, exponential and log

Unit 11 Transformations and Parent Functions

67 Graph absolute value functions
68 Horizontal and vertical translations of linear, quadratic, cubic, abs value, exponential and log
69 Reflections and stretching of linear, quadratic, cubic, abs value, exponential and log
70 Combinations of transformations on parent functions
71 Identify parent graphs of parent functions
72 Identify equations of parent functions

Unit 12 Conics

73 Identify a conic from graph
74 Identify a conic from equation

Unit 13 Variations

75 Write equation for direct, inverse and joint variation problems
76 Find the constant of variation

Unit 14 Sequences/Series

77 Write n terms of an arithmetic sequence
78 Find the sum of a finite arithmetic series
79 Write n terms of geometric sequence
80 Find sum of geometric series
81 Use formulas to find nth term
82 Identify sequence/series as arithmetic, geometric or neither

Unit 15  Statistics

83 Determine probabilities associated with areas under the normal crve
84  Compute permutations and combinations

 
If you made it this far, here's my call for help:  Anyone have advice/suggestions for how to make this work and/or a better way to organize the information into cohesive units that seem to occur in a somewhat logical order?  There is and will continue to be an emphasis on function families and transformations (as there should be).  I find it difficult to express on paper how each function category needs to be a resting place, but they are all connected in the ways that transformations apply.  Any ideas?
 
...oh...and I'm going to be teaching one section of deaf students and one section of blind students...in case that makes a difference

**edit:  I've added links to the old and new Virgina SOLs for Algebra 2 if anyone's interested**

Factoring cubic polynomials

The Amazing Housefly Part 2: Coolest Eye Ever

As longtime readers know, I am fascinated by vision, and find it absolutely fabulous that the world is bathed- all day long- in electromagnetic radiation that bounces around all over the place and reflects off of practically everything.

I’m even more amazed that we have these funny little camera-like balls stuck in our faces with refractive lenses that focus this reflected radiation onto little screens set back in our heads, and that these screens, and the neural circuitry wiring them up to our brains, can turn this jumble! of a gazillion different photons of different wavelengths and intensities into a full-blown 3-dimensional model of the world around us, extending from a few inches in front of our nose to dozens of miles away.

Think about that the next time you’re down in the dumps. You can see! Think about what an amazing, incredible, impossible thing that is, and you do it all the time without thinking about it. Sometimes we worry about work or family or the meaning of life or whatever, but if you step back and think about it- really think about it- the mere fact that you can actually see makes your whole life worth it even if! you never accomplish anything else. Everything else in life i! s gravy.

I’m also fascinated by how other living creatures see, and how the world appears to them. So much of our sense of the world is wrapped up in how we see it, as is- I’d argue- our sense of self. Think about how you sense yourself. If you really think about where you are, in your body, it’s not in your hand or your leg or your belly- it’s in your head, right behind your eyes.

We’ve looked at the vision of other creatures before, including birds and other mammals. But all of the eyes we’ve looked at are camera-style eyes, very much like our own. Camera-style eyes are just one of several basic eye “architectures”, and by no means the most prevalent. No, the most common eyes in the world are compound eyes, and the trillions of creatures who bear them see the world very differently from you and me.

In a human eye (diagram right, not mine*)! , light passes through the cornea, and enters the eyeball thro! ugh a le ns which focuses the image, via refraction**, onto the back of the eyeball, or retina, where the various wavelengths of light received aan recognized by special receptors which communicate this information to the optic nerve. There’s a lot more detail, but that’s how it basically works, and the same general design is present in the vast majority of land-based vertebrates. There are plenty of differences between animals of course. For example, the shape of our eyes’ lenses is somewhat flexible, allowing us to focus on objects near or far. But some animals, such as snakes, have lenses that are fixed, and focus by effectively telescoping the lens***.

*Because hell, I already drew enough graphics for this post

**I explained refraction in this post.

***Arguably making them much more “camera-like” than ours.

There are also invertebrates- namely spiders- that have camera-style eyes, but the overwhelmingly majority- including Flies- have compound eyes. There are several different types of compound eye, but the most common design among insects is the Apposition Compound Eye. Here’s how it works.

A compound eye consists of multiple (from as few as 6 to as many as 30,000) individual “eye units” called ommatid! ia. Each ommatidium consists of a hexagonal tube capped by! a teeny little cornea. Just below the cornea is a teeny little crystalline lens-cone, and just below that is a photo-receptive organelle called the rhabdom, and which consists of a small number of individual photoreceptor cells, called rhabdomeres, fused together toward the bottom of the tube. The light-data received by the rhabdom is transmitted through a single axon, or nerve fiber, which transmits the image to a succession of nerve layers (the lamina, medulla and lobula) where it’s combined with the thousands of other images being received simultaneously from other ommatidia and combined into a composite image in the insect’s brain.

You need to remember this part, or you’ll be lost when we get to the Fly-Eye. Go back and read it again if it didn’t make sense.

Tangent: There’s a cool parallel here with the plant world- composite flowers. Just as a daisy or a dandelion is composed of hundreds of miniaturized flowers, a compound eye is composed of hundreds (or thousands) of “mini-eyes.”

An apposition-eye image is generally not as precise as a camera-eye image. Part of this is due to the effects of diffraction* in the small opening of the tube; it’s likely that most (all?) insects cannot see stars in the night sky. So insects that need really good vision have lots and lots of ommatidia- close to 30,000 per eye in some Dragonflies. Even so, a Dragonfly’s image of the world is far less precise than ours.

*I haven’t explained diffraction in this blog, and unfortunately this post is long enough. If you’d like an explanation right now, you can check out the Wikipedia entry for (a longer than necessary) one.

Side Note: Many apposition-eye insects, such as dragonflies and drone (male) bees*, have areas of the eye with “acute” vision characterized by larger facets which help mitigate the effects of diffraction. This “acute vision” portion of the eye is analogous to foveal vision in birds.

*Drones have better eyesight (and flight-speed) than workers or queens, since pretty much the only thing they do in life is intercept a flying queen to mate.

But the apposition-eye has a couple of advantages over our camera-style eyes.

The first has probably already occurred to you- the field of vision can be huge. A Dragonfly for example has a nearly 360 degree field o! f vision.

Extr! a Detail : And that understates it. It’s 360 degrees (or close to it) with respect to a 2-dimensional plane. But the dragonfly is seeing up and down as well in a total field of vision that is nearly spherically 360 degrees. As if that weren’t enough, Dragonflies see more colors than we do; most are tetra- or pentachromatic*. In particular Dragonflies seem to have enhanced color sensitivity in the blue-to-ultraviolet range. It’s thought that this “brightens” the sky and makes prey insects stand out more clearly.

*This applies to day-flying Dragonflies. Many species are active only around dusk, and it’s not entirely clear what color-vision capabilities they have.

BTW, when I was doing this post I dug around in through some old photos for a Dragonfly* pic. This one’s from June, 2005, up the South Fork of Dry Creek. If you’re a Salt Lake-area trail-user, this is the major fork off to the right as you climb Dry Creek, about ½ way up. It’s a big, deep, seldom-hiked canyon, much d! eeper than Dry Creek proper, with a year-round stream. The day! I hiked it the canyon was filled with these amazing-looking black & orange dragon flies, and I snapped a few pics (with, unfortunately, a lesser camera than I have today.) I filed it away and forgot about it.

*Dragonflies are of course Way Cool, and I intend to post about them next Spring/Summer.

Anyway I dug them up this week and think I ID’d it as a female Twelve-Spotted Skimmer, Libellula pulchella. Is she gorgeous or what?

The second benefit is that the apposition-eye forms and processes images much more quickly than a camera-style eye, which translates to a much, much higher flicker rate.

Humans have a flicker rate of roughly 50 to 60Hz, or images per second, and in fact if we see more than about 30 images per second we perceive constant motion. This is why old-style fluorescent lighting caused headaches; the refr! esh rate of the bulbs was only about 60Hz*. But other animals have different, and often higher, flicker rates. Most birds for example have flicker rates in excess of 100Hz, which is one reason they’re able to fly in and amongst tree limbs without colliding with branches all the time.

*This is not a problem with modern CFL bulbs, which have a refresh rate in excess of 10KHz.

Tangent: Know what other animal has a higher flicker rate than us? Dogs. In fact if you’re reading this on an old-style CRT monitor, and your dog is with you in the room, there’s a good chance that he/she sees your screen flickering right now. Most CRT displays are set to 70-90Hz. Dogs have flicker rates as high as 80Hz.

This also the case with CRT-design television sets, but not with modern flat-panel monitors or TVs, which have refresh ra! tes of around 200Hz, and don’t really refresh the same w! ay anywa y.

But large-eyed flying insects have flicker rates in excess of 200Hz, which is incredibly useful when you’re in fast flight, chasing down another fast-moving, highly-maneuverable, flying insect.

So a Dragonfly or a Bee sees the world less precisely than we do, but they see far more of it and more real-time than we do. To a certain extent, they think faster.

Side Note: This BTW is the real reason it’s so darn hard to swat a fly. Yes, they can ride out the wind-wave pushed ahead by your hand or magazine coming down to swat them, but they have to be ready- and actually jump- to catch that wave. A Housefly can move into jump-ready/take-off position in 100 milliseconds, which is just 1/3 of the time it takes your brain to tell your hand to “swat.”!

Refraction Superposition

So apposition-eyes have some real advantages, but they’re not the only kind of compound eye. Moths, for example have a completely different type of compound eye.

Moths, as you’ve probably noticed, are active at dusk and in the evening, when very little light is available. So they need eyes with an architecture that makes the most of what light they do receive. Moth eyes don’t aggregate images like Dragonfly eyes, but rather superimpose multiple images through a technique called refract! ion superposition.

While a moth’s eye looks supe! rficiall y similar to an apposition eye, internally it’s radically different. Light is refracted through the lens element of each ommatidium in such a way that it emerges from the bottom of that ommatidium at the same angle, and then onto a teeny little retina.

So in a weird way, it’s- internally at least- a little bit more like our eye. The ommatidium achieves this by acting like a two-lens telescope, which it accomplishes by containing a cylindrical lens with a gradiated refractive index that continually bends the light as it travels through the tube. In other words, the refracti! ve index of the lens varies depending on where it is along the tube. (This is way, way cooler than your telescope.)

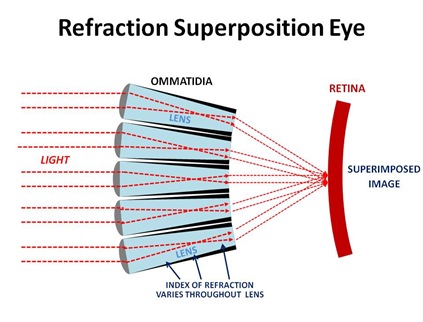
The guys who figured this out BTW, an Austrian physiologist names Sigmund Exner, did so way back in the 1880’s, but it wasn’t until the 1970’s that sophisticated-enough instrumentation* was developed to prove him right.

*The interference microscope.

Reflection Superposition

Superposition is such a great idea that it’s evolved multiple times in compound eyes, using very different architectures. Lobsters for example, also live in light-poor environments where superposition helps improve image formation. But refractive lenses are trickier to effect in water, which has a much higher refractive index than air. So the lobster’s eye achieves superposit! ion via reflection. The insides of a lobster’s ommatidia! are mir rored, and each facet uses reflection internally to focus the image onto the teeny retina.

More recently (1988) a third type of superposition compound eye was discovered in a genus of crabs (Macropipus) that use both crystalline lenses and parabolic mirrors, and is called the Parabolic Superposition Eye. Superposition eye of all (optical) types BTW need to be very spherical in form to superimpose the images correctly.

Wow. That’s a lot of cool bug-eyes. But what does all this have to do with flies?

Everything. Bec! ause flies have the coolest* compound eyes of all.

*Totally my opinion, and I have absolutely no authority or credentials to back it up. But it’s true. Really.

Neural Superposition

A fly’s eye is structurally very similar to an apposition eye, like a dragonfly’s or a bee’s.

But it’s wired differently. It’s also a superposition eye, but it achieves superposition neurally! . Remember when we walked through the structure of the apposit! ion eye, after the images were received by the 8 rhabdomeres, or photoreceptor cells, they were joined into a single rhabdom which was connect by a single axon, or nerve fiber, to the lamina, or top nerve layer below.

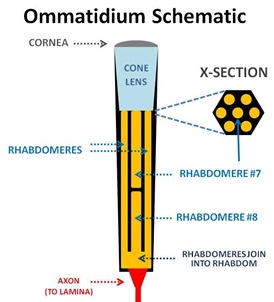
But in a neural superposition eye, the rhabdomeres stay separated clear down the tube, and emerge from the bottom as 7* separate nerve fibers, each of which is then joined at the lamina to 6 other fibers from rhabdomeres from the 6 adjoining facets surrounding it which are angled in the same direction**. So the image received at the lamina is 7 times brighter than the image at any given photorece! ptor, which helps flies form superior images in low light conditions. And because superposition is achieved via wiring (vs. optics) the shape of the eye doesn’t need to be as strictly spherical, allowing for greater flexibility of form. Neural superposition eyes are are also thought to be even more sensitive to motion detection than apposition eyes and might experience an improved signal-to-noise ratio.

*There are 8 rhabdomeres, but #7 and #8 sit on top of each other in the center, and are effectively one.

**The angles between individual rhabdomeres in a given ommatidium are the same as the angles between adjacent ommatidia.

Now that’s a cool eye.

Halteres, pulvilli, neural superposition eyes- they’re just 3 of a whole slew of amazing features in Houseflies. As is over and over again the case in this project, each little living thing turns out to have this amazingly cool story when you stop, check it out and learn a little bit about it.

Here’s something kind of gross about me: I routinely swat bugs with my bare hand. I’m not proud of it, but a couple of my apartments in college were so bug-infested that if I’d had to search for a tissue or swatter every time I spotted a roach, I’d never have managed to eek out a degree in 4 years. The habit’s stuck, and over the years I’ve become not-half-bad at hand-swatting flies. But this gal had been a fine subject, posing patiently on my driver’s-side window as I fumbled with focus and lighting to get my shot. I opened the car door, gently shooed her out, and walked across the lot to my office.

Compound and Multiple Angles